オイラー、リーマン、ラマヌジャン 黒川重信 岩波科学ライブラリー ★★★☆☆
ζ(2) = 1 / 12 + 1 / 22 + 1 / 32 + ... = π2 / 6
夜(月)の世界:
ζ(-1) = 1 + 2 + 3 + ... = -1/12
こういう具合に、ζ(s) と ζ(1-s) との間に対応関係が成り立つ。sが0と1の間は、トワイライト・ゾーンである。ゼータの虚根は、闇と光の世界の中心線である s = 1/2 にしか存在しえない、というのが有名なRiemann予想である。
またゼータは、Hasse、Langlands、Artin、Selbergという4つの異なる姿をとってわれわれの前に立ち現れる。この4つのゼータを統一するのが、21世紀の「絶対数学」の夢である。これは、物理学における4つの力の統一の夢と奇妙な符合を見せる。(ただし、本書に出てくる生物との対応はメチャクチャなので、そこは無視する。)
x以下の素数の数 π(x) を与えるRiemannの素数公式があまりにも美しいので、ここに記しておく。
ここで、
μ(m)はMöbius関数で、mが平方数で割り切れるときは0、mが異なるk個の素因数に分解されるときは (-1)k である。ρはゼータの全ての虚根を動く。しかも、これはmについての無限和になっているので、この公式から例えば π(100)=25 がどのように計算されるのか、皆目見当がつかない。
3章から突如として難解になる。ここをもう3倍くらい詳しく記述して欲しかった。
個人的には、ラマヌジャンこそは人類史上最高の天才だと思っている。ラマヌジャンのτとか2次のゼータを理解するには、保型形式について勉強しなければならない。それはまた、有限世界での楕円曲線の解の個数とも関連していて、Fermat-Wilesの定理の証明の要となった谷山-志村予想(「すべての楕円曲線はモジュラーである」)とも密接に関わっている。
やはり、数論の世界には絶対的な美がある。と言うわけで、またまた懲りずに数論の勉強を開始しようと思い立った次第。(09/02/28 読了)

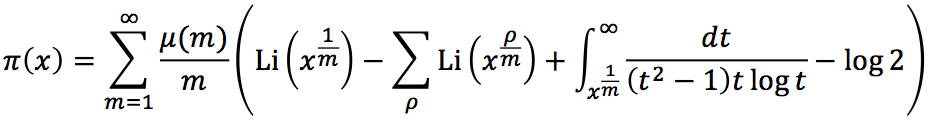
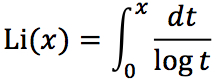
 読書日記 2009年
読書日記 2009年 