ポリオミノの宇宙　ソロモン・ゴロム　日本評論社　★★★★☆

ポリオミノ（polyomino）とは、いくつかの同じ大きさの正方形を辺同士でつなぎ合わせた図形のことである。
正方形を１個、２個、３個、４個、５個、･･･、つないだ形はそれぞれモノミノ（monomino）、ドミノ（domino）、トロミノ（tromino）、テトロミノ（tetromino）、ペントミノ（pentomino）･･･、と呼ばれる。これは、正方形を２個つないだ形状が「ドミノ」（domino）であることから、これを d + omino と分解して頭の "d" をギリシャ語で２を表す接頭辞（di-）と解釈したものである。（transcriptome、metabolome みたいなものだ。）
ちなみに、「テトリス」で上から降ってくるのは、テトロミノである。

本書は、ポリオミノの生みの親であるソロモン・ゴロム（Solomon Golomb）の手によるものである。
ゴロムは1953年、大学院生の時にポリオミノを「発明」した。非常にシンプルで、小学生でも容易に理解できるにもかかわらず、その背後には組み合わせ論の深淵な世界が広がっている。まさに「宇宙」と呼ぶに相応しい。
優れたアイディアというのは、シンプルだけれども、新しい世界を丸ごと生み出すものである。

回転・裏返しで重なるものは同形と見なすと、ペントミノは全部で12種類ある。
この12種類のペントミノを6×10の箱に詰めるパズルが「プラパズル」の名前で現在でも市販されている（昔はもっとたくさん種類があったのだが）。
私は小学生の時に、担任の先生にこのパズルを教えてもらってすっかり魅せられてしまい、独力・手動でヘキソミノ35種、ヘプトミノ108種、オクトミノ369種を数え上げた。
この話は、（私の名前と共に）その先生の著書である『算数的思考法』（坪田耕三、岩波新書）に出てくる。

n-ポリオミノが何種類あるか、正確に数え上げる公式は知られていない。
現在のところ、白川俊博さんという方によって n = 45 まで数え上げが完了しているようである。
その数列 P(n) は、1, 1, 2, 5, 12, 35, 108, 369, 1285, 4655, ...と続く。 P(45) の値は

2,155,600,091,107,324,229,254,415 (= 2×10²⁴)

である。（その完全な数列はこちら。）
ちなみに OEIS (The On-Line Encyclopedia of Integer Sequences) というサイトには、様々な整数列が網羅してあって非常に楽しい。

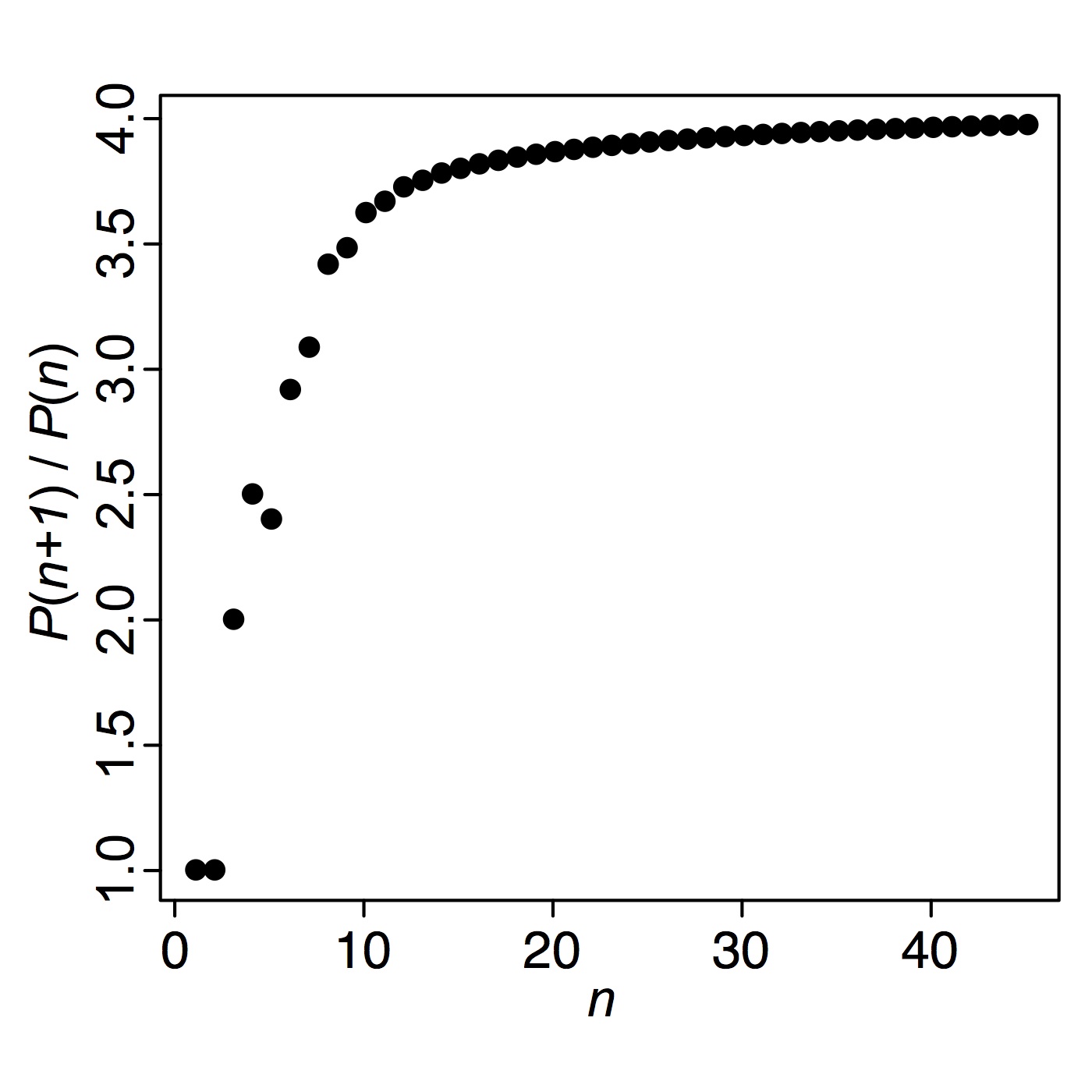P(n+1)/P(n) の値は、少しずつ大きくなりながら４あたりに収束するように見える（左図）。実際、P(n+1)/P(n)はある値 λ （クラーナー定数、Klarner's constant）に収束することが知られており、4.00 < λ < 4.65 が証明されている（Prof. Gill Barequet's home page）。

本書は、構成の不可能性を証明するためのバックトラックと呼ばれるアルゴリズムや、数え上げ理論におけるポリア（Polya）の定理にも言及されていて、教育的である。
しかし何より、ヘプトミノ、オクトミノ、ノノミノによる巨大な敷き詰めのパターンは、眺めているだけで楽しい。1960年代から70年代という時代に、一体どうやってこんなパターンを見付けることができたのだろうか？人力で発見したとしたら驚異的である。
三角形、六角形、立方体への拡張はすぐに思い浮かぶが、準ポリオミノ、擬ポリオミノというのは知らなかった。４次元以上への拡張も面白そうだが、４次元ポリオミノの４次元空間での箱詰めは、直感的に把握できないのであまり流行らないかもしれない。

同形のポリオミノによる敷き詰め問題は奥が深い。Michael Reidのサイト に最新の結果がまとめられている。
本書に載っていない、新しい興味深い問題として、別種のポリオミノで最小面積の同じ形を敷き詰める問題（「最小公倍図形」問題）や、非対称なポリオミノで対称な形状を作る問題などがある。例えば、Lペントミノ、Pペントミノ、Xペントミノで敷き詰めることができる、知られている最小の図形は、左図のような80個のペントミノからなるものだ（Triple Pentominoesより）。
これらの問題に関しては、Col. George Sichermanのサイト や Livio Zuccaのサイト に結果が網羅されているが、まだまだ未解決問題がたくさんありそうである。

この手の問題はれっきとした離散数学の研究対象で、学術論文も多数書かれているが、日本にはこういう分野の研究者がほとんどいないようなのは残念なことである。日本の数学界ではあまり推奨されていないのかもしれない。

原著の初版は1964年に出版されたが、邦訳は存在しないようである。本書は2014年に出版されたばかりだが、原著（改訂版）はその10年前に出版されたため、内容がやや古くなってしまっている。とはいえ、初版から半世紀の歳月を経てようやく日本語版が出版されたのは喜ばしいことだ。（15/03/11読了 15/03/22更新）