ひとけたの数に魅せられて マーク・チャンバーランド 岩波書店 ★★★★★
これは楽しい!こういうの大好き。
数にまつわるウンチクを集めた本は巷にたくさんあるが、本書は1から9までの一桁の数だけに絞ったことで、個々の話題について理論的な背景まで掘り下げて書いてある。
扱っている内容は多岐にわたり、かつレベルが高い。数の話題だけでなく、一見してへぇ!というような初等幾何の話題もバランスよく収められている。知らないことがたくさん書いてあった。
この手の本に割とありがちな、西欧文明にバイアスがかかった数学的に無意味な話題(例えば、「3」ならばキリスト教の三位一体説とか、13が不吉な数とか)を徹底して排除しているところも良い。
ちょっと気になったトピックについて、キーワードだけ列挙しよう:
シェルピンスキーのガスケット/スー-モース数列/アポロニウスの円の充填/コラッツ予想(3x+1問題)/モーリーの奇跡/フバータルの櫛/マーデンの定理/オイラーの冪乗和予想/ヴィラソーの円/ミケルの5点円定理/ロジャーズ-ラマヌジャン恒等式/ケルヴィン予想とウィア-フェラン構造/球の首飾り(江戸時代の算額にも登場する!)/7円定理/7分の1楕円/シラッシ多面体/ファノ平面/ピザ定理/神秘六芒星定理/フェルマー-カタラン予想/ヘーグナー数とラマヌジャン定数(= e π√163)・・・
数学というと無味乾燥なものだと思われがちだが、ネーミングからして文学的ではないか。
自分への備忘録も兼ねて、いくつかの話題についてもう少し詳しく書いておこう。
シラッシ多面体
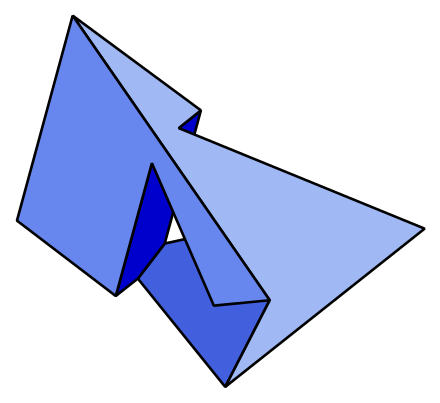 シラッシ多面体(Szilassi polyhedron)とは、7つの6角形からなる、ドーナツのように穴の空いた7面体である。14個の頂点、21本の辺をもつ。
シラッシ多面体(Szilassi polyhedron)とは、7つの6角形からなる、ドーナツのように穴の空いた7面体である。14個の頂点、21本の辺をもつ。
興味深いことに、すべての面が、自分以外のすべての面と接している。このような性質をもつ多面体は、ほかに4面体しかない。
シラッシ多面体はまた、トーラス(ドーナツ)上の地図の塗り分けに7色が必要であるという最小の例にもなっている。
ここに詳しい解説がある。
ロジャーズ-ラマヌジャン恒等式と整数の分割
ロジャーズ-ラマヌジャン恒等式(Rogers–Ramanujan identities)は、次の美しい公式である。
これらの恒等式は、一見すると何の関係もなさそうな、「整数の分割」の問題と密接に関連してる(qnの係数がnの分割数を表しているからだ)。
この式から、分割数に関する次の定理が導かれる:
(1) どの構成要素の差も2以上であるような分割の仕方と、すべての構成要素が5を法として1または4と合同(5で割った余りが1または4)であるような分割の仕方は等しい
(2) 構成要素がすべて2以上であり、かつどの構成要素の差も2以上であるような分割の仕方と、すべての構成要素が5を法として2または3でと合同あるような分割の仕方は等しい
実際、例えば9に対する分割を考えると、前者は
9 = 8 + 1 = 7 + 2 = 6 + 3 = 5 + 3 + 1
1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = 1 + 1 + 1 + 1 + 1 + 4 = 1 + 1 + 1 + 6 = 1 + 4 + 4 = 9
となってどちらも5通り、後者は
9 = 7 + 2 = 6 + 3
2 + 2 + 2 + 3 = 2 + 7 = 3 + 3 + 3
でどちらも3通りとなる。
(参考:『整数の分割』ジョージ・アンドリュース、キムモ・エリクソン 数学書房)
オイラーの冪乗和予想
オイラーは、フェルマー予想で n = 3 の場合、
x3 + y3 = z3
に整数解がないことを証明した。そこでオイラーは、
x1k + x2k + ... + xnk = zk
において、n < k のときには整数解は存在しないと予想した。
しかし、オイラーは間違っていた。1966年に、コンピュータによる網羅的探索によって、次の反例が見つかったのだ。
275 + 845 + 1105 + 1335 = 1445 = 61917364224
さらに1986年には、弱冠20歳のノーム・エルキーズ(Noam Elkies)が、k = 4 に対する驚くべき反例を発見した。同時に、解が無限個存在することも証明された。
26824404 + 153656394 + 187967604 = 206156734 = 180630077292169281088848499041
フェルマー-カタラン予想
これもフェルマー予想の拡張版である。次の方程式を満たす整数解は有限個しかない、という予想だ。
xp + yq = zr
ただし、x, y, z は互いに素で1より大きく、1/p + 1/q + 1/r < 1 を満たすものとする。
これに対する解は、現在までに次の9例しか見つかっていない:
25 + 72 = 34 = 81
73 + 132 = 29 = 512
27 + 173 = 712 = 5041
35 + 114 = 1222 = 14884
338 + 15490342 = 156133 = 3805914951397
14143 + 22134592 = 657 = 4902227890625
92623 + 153122832 = 1137 = 235260548044817
177 + 762713 = 210639282 = 443689062789184
438 + 962223 = 300429072 = 902576261010649
これら9例の出現頻度がひどく偏っているように見える(2例が13桁、3例が15桁の数)のも不思議だ。
これは、まれにしか出現しない完全冪乗数がどのように分布しているかという問題で、ABC予想と密接な関係がある。ABC予想が肯定的に解決したことにより、そこからフェルマー-カタラン予想も導かれることになる(らしい)。
(16/06/13読了 16/06/19更新)

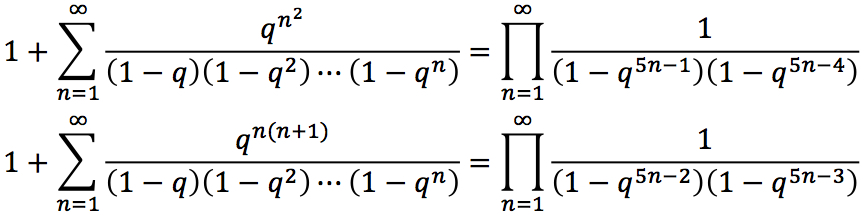
 読書日記 2016年
読書日記 2016年 