代数方程式のガロアの理論　Jean-Pierre Tignol　共立出版　★★★★☆

翻訳はひどいが、内容は素晴らしい。英語の語順そのままに、逐語的に日本語に置き換えたような文体なので、読んでいてストレスが溜まる。しかし幸いにして、数学の証明は言語に依存しないため、それが致命的な欠点というわけではない。

本書は、数学の本であると同時に、数学史の本でもある。数学を理解せずに数学史を語るのは、語学を学ばずして言語学を語るようなもので、片手落ちである。
数学の本というのは、定理と証明が延々と続く教科書か、厳密性を犠牲にした読み物のどちらかが大部分だ。両者をバランスよく含む本というのはほとんど存在しないが、本書はその数少ない例外である。
本書はまた、その時代に知られていた数学の道具だけを使って説明しているところが良い。
そのため、後半に行くにつれて指数的に難しくなっていく。証明を一つ一つフォローしていかないとたちまち行き詰まるので、決して容易に通読できる本ではない。
しかし、行きつ戻りつ、呻吟しながらじっくりと読み進めていけば、以前はよく分からなかったところも、霧が晴れるように理解できるようになってくる。「読書百遍意自ずから通ず」なのである。

方程式の歴史は古い。紀元前2000年、楔形文字で刻まれたバビロニアの粘土板に、既に2次方程式の解法の説明があるという。
しかし、3次方程式の解法が得られたのは1515年ごろであり、2次方程式に比べてはるかに難産だった。
ここで注意しなければならないことは、16世紀の数学者は、今日我々が用いているような、方程式を書き表す記号を持っていなかったということである。そのため、3次方程式の解法は、詩の形で伝えられた。

立方といくつかのものの和は1つの数に等しい。2つの数の差が与えられた数であり、それらの積がいくつかのものを表す数の3分の1の立方に等しい2つの数を見つけよ。このとき、これらの2つの数の立方根の差が未知数である

3次方程式の解法は、未知数をわざわざ2つの未知数の和に分解するところがミソなのである。なぜそうするとうまくいくのか。そのことの意味は、本書を読み進めていくと少しずつ明らかになってくる。

個人的には、第12章「ガウスの円分方程式」が大変勉強になった。
任意の素数 p に対し、1の p乗根 ζ_i はベキ根で表すことができる：

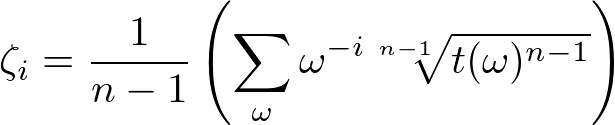
ここで、g を p の原始根とするとき、

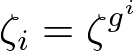
と定義する。ω は1の p-1乗根であり、総和はすべての ω を動く。また、t(ω) はラグランジュ分解式

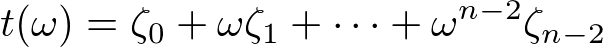
である。このように、1の p乗根は1の p-1乗根で表すことができるのだ。
ただし、この計算を実行するのはかなり困難である。

本書には、ヴァンデルモンドによって計算されたという、1の11乗根の値が載っている（その値はこちら）。11 - 1 = 2 × 5 だから、1の11乗根を求めるためには5次方程式を解く必要があり、1の13乗根を求めるのよりもずっと難しい。
一方、17 - 1 = 2⁴（つまり、17はフェルマー素数）だから、1の17乗根は平方根だけで書き表せる。実際、その実部は

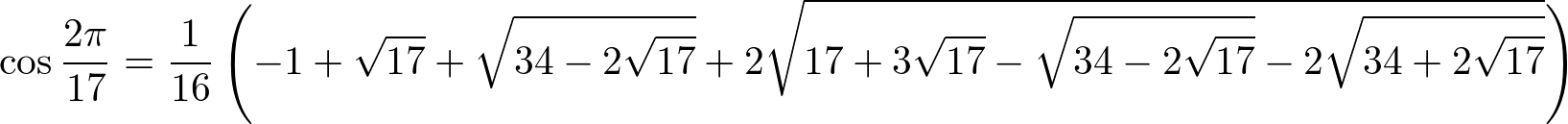
という例外的にシンプルな値になる。
弱冠19歳のガウス青年がある朝目覚めたときに、定規とコンパスだけで正17角形を描く方法を思いついた、というのは有名な話である。それは、加減乗除と平方根だけで書き表せるような座標を平面上にプロットするということに他ならない。ここに実際の作図方法が載っている。

続く第13章「一般方程式におけるルフィニとアーベル」において、5次方程式の解法の不可能性が証明される。それは不可能の証明だから具体例を挙げることはできず、議論は次第に抽象度を増していく。
そして最終14章においてガロア理論が記述されるが、ここではアルティン流のガロア拡大やガロア対応を用いた議論でなく、ガロアの元論文に近いやり方で説明してある。そのためこの章が一番長いのだが、証明をフォローする気が起きない。第一、ガロア群の定義からして分かりにくい。

しかし、5次方程式が解けないことを理解するだけなら、アーベルの証明で充分なのである。
5次方程式に解の公式が存在しない理由が気になって、まず『群の発見』（原田耕一郎）を読もうと試みたが、途中で挫折した。それから『群論への30講』を経て、さらに本書を通読することで、ひとまず目標は達成されたのだ！
→ 5次方程式が解けないことの直感的説明
ガロアは、方程式論に完全に終止符を打つとともに、群論というまったく新しい世界への扉を開いた。ガロア理論は、別の本で改めて勉強することにしよう。 （17/04/13読了 17/04/18更新）